klik om te vergroten

XX Van kaart aan de wand naar wandkaart: Generalisering van schoolwandkaarten vanaf 1840

door Lowie Brink

Een mea culpa is hier eigenlijk wel op zijn plaats. De auteur beweert al jarenlang dat schoolwandkaarten in de 19de en 20ste eeuw steeds soberder werden, dat de afstandswerking verbeterde, dat de volledigheid aan de duidelijkheid werd opgeofferd, etc. Allemaal kwalitatieve uitspraken, maar nooit eens een echt kwantitatief bewijs. Is het echt wel zo, en zo ja hoe snel ging die veronderstelde 'versobering' dan wel? Met dit artikel wordt geprobeerd een en ander weer recht te zetten. Enige passieve kennis van het Duits bij de lezer is wenselijk aangezien geput is uit kamers vol Duitstalige, kartografische vakliteratuur.

SOLCHER UNLESERLICHKEIT

Leesbaarheid van kaarten en overlading staan op gespannen voet met elkaar. In een boek met de klinkende titel Grundsatzfragen der Kartographie luidt het dan ook: "Überlastung des Kartenbildes ist ein der Hauptprobleme der kartographischen Gestaltung." [Bobek, 1970] In Nederland geven de kaartseries van de Topografische Dienst mooie voorbeelden van een dergelijke overbelasting. Ze werden vanaf de 19de eeuw "volgestouwd" om toch maar zo veel mogelijk informatie erin op te slaan. Desondanks werden ze "zonder protest geaccepteerd". [Commissie, 1973] Gebruikers konden indien nodig toch wel even een vergrootglas erbij pakken? Maar volgens de Zwitserse kartograaf Imhof - toch niet de eerste de beste - is dat niet de bedoeling: "Es ist falsch die Minimaldimensionen dem Kartenlesen mittelst Lupe anzupassen." [Imhof, 1972] Hij had daarvoor ook al zijn ongenoegen geuit: "In manchen Karten der letzten 150 Jahre vermag selbst ihr geübtester Benützer das Gewirre von Strichen, Signaturen, Farben und Buchstaben nicht zu entwirren." [Imhof, 1967] Het geklaag over 'visual clutter' is dan ook een steeds weer terugkerend fenomeen. Het feit dat er doorgaans geen aandacht was voor de kaartgebruiker kan verklaren waarom er nog zo lang en zo veel overvolle kaarten zijn vervaardigd. Maar de democratiseringsgolf van de jaren '60 lijkt ook in kartografenland zijn sporen te hebben achtergelaten: "Tot 1970 hebben kartografen zich te weinig aangetrokken van de eisen waaraan kartografische kommunikatie moet voldoen." [Ormeling, 1972] En de Tsjechische kartograaf Kolácný schreef in zijn beroemd geworden artikel over een kartografisch informatiemodel: "One would hardly believe how little attention has been given until recently to the theory and practice of map use." [Kolácný, 1969a] Hét middel tegen overvolle kaarten is natuurlijk kartografische generalisering. Hieronder zal daarop kort worden ingegaan en vervolgens op de generalisering van schoolwandkaarten. Want ook van de gebruikers van sommige schoolwandkaarten - leerlingen maar ook onderwijzers en leraren - leek wel verwacht te worden dat ze vergrootglazen en verrekijkers erbij zouden pakken.

JEDES KARTENZEICHNEN IST EIN GENERALISIEREN

Kartografische generalisering is een van de kernhandelingen van de kartografie en wordt dan ook al eeuwenlang toegepast. De toename van de topografische kennis in de eerste helft van de 19de eeuw maakte dat generalisering steeds noodzakelijker werd. Dit was dan ook de tijd dat de term generaliseren gangbaar werd, ook al gebruikte een pionier op dit gebied, E. von Sydow, in zijn baanbrekende artikel Drei Karten-Klippen [Sydow, 1866] nog de term 'Verkleinerung' ("eine Klippe welche alle Elemente der Karte berührt, und an welcher schon Viele gescheitert sind.") Pas in 1910 zou A. Hettner weer trachten de generalisering te doorgronden met uitspraken als: "Die Vereinfachung kann als Weglassung, oder die Weglassung umgekehrt als Vereinfachung aufgefaßt werden." [Hettner, 1910] En wat later zou M. Eckert in zijn monumentale Die Kartenwissenschaft aandacht besteden aan generalisering ("Diese is gemeinhin das Kriterium guter und brauchbare Karten. … Die Ausführung unterliegt ganz und gar dem Können und Kennen des Kartenzeichners.") [Eckert, 1921] Met de opkomst van de kartografie als wetenschap vanaf de jaren '50 nam ook de aandacht voor generalisering toe. Daardoor is ook de lang stand gehouden opvatting van Eckert e.a. - generalisering is een subjectieve bezigheid en is niet in objectieve, wiskundige regels te vangen - aan het wankelen gebracht. [Töpfer, 1974] Eckert zou op de diverse congressen over 'automated generalization' met grote ogen hebben rondgelopen.

SCHULWANDKARTEN ÜBERTREIBEN MIT VOLLEM BEWUßTSEIN

De 'uitvinding' van de schoolwandkaart in de eerste decaden van de 19de eeuw had - onbedoeld - revolutionaire trekjes: "Sie hat einen Emanzipationsprozeß eingeleitet der endlich den 'gemeinen Mann' mit dem Weltbild erstmalig bekannt und vertraut machte." [Sperling, 1986] De hierboven al genoemde E. von Sydow, een docent aan een militaire academie, was een van de aanstichters van deze beweging. Hij sprak zich niet alleen als een van de eersten uit over generalisering, maar paste vanaf 1838 zijn denkbeelden ook toe in sterk en knap gegeneraliseerde schoolatlassen en schoolwandkaarten. "Aan E. von Sydow hebben wij het te danken, dat het onderwijs in de aardrijkskunde thans in den waren zin des woords klassikaal en aanschouwelijk kan gegeven worden." [N.N., 1853] Het goede voorbeeld van Von Sydows schoolwandkaarten ten spijt, leidden echter alle Nederlandse schoolwandkaarten uit de eerste helft van de 19de eeuw aan een groot euvel: overladen en van een afstand niet duidelijk. Tussen de kritiekloze en blijmoedige recensies van deze kaarten in Nederlandse onderwijsbladen komt de modern aandoende, zeer kritische bespreking van de Leidse hooglereaar P.J. Veth verfrissend over: "De kaarten moeten derhalve op zeer groote dimensiën geteekend zijn, en toch slechts het allervoornaamste bevatten." [Veth, 1852] De overlading was waarschijnlijk een gevolg van het feit dat al eeuwenlang "ein Unterschied zwischen Handkarten und Wandkarten zunächst nicht gemacht wurde." [Sperling, 1986] Pas aan het eind van de 19de eeuw werden duidelijke eisen geformuleerd waaraan effectieve schoolwandkaarten moesten voldoen, zoals in Nederland door J.J. ten Have en H. Zondervan. [Brink en Holl, 2010, p. 31-33] In het kaartontwerp moet een afstandswerking van ca. 2 tot 8 m centraal staan: "eine relativ beschränkte Auswahl der darstellbaren Objekte in sehr deutlicher, übertreibender Hervorhebung." [Witt, 1970, p. 1061] Om na te kunnen gaan in hoeverre deze aanwijzigingen in de Nederlandse schoolwandkaarten verwerkt zijn, zullen we eerst methoden moeten vaststellen om de generalisering te kwantificeren.

QUANTITÄT DES KARTENINHALTES

Generalisering is een breed begrip en één kwantitatieve maat is daarvoor niet te geven. Maar de met generalisering verwante term (optische) leesbaarheid geeft echter aanknopingspunten. Deze wordt namelijk bepaald door het aantal kaartobjecten, de vorm en grootte van de symbolen en het contrast. [Bertin, 1974; Ormeling, 1997] Hiervan zijn het aantal objecten (door de kaartbelasting) en de grootte van de symbolen (door de ooghoek) eenvoudig te kwantificeren. Kaartbelasting en ooghoek zullen hieronder worden uitgewerkt. Dat we met deze twee begrippen de generalisering voor een belangrijk deel kunnen karakteriseren blijkt als we kijken naar de zeven handelingen van generaliseren: vereenvoudigen, vergroten, verplaatsen, samenvoegen, selecteren, symboliseren en benadrukken. [Ormeling en Kraak, 1987] Selecteren ("die wichtigste und primäre Generalisierungsmaßnahme" [Töpfer, 1974, p. 191]), vereenvoudigen en samenvoegen bepalen grotendeels de kaartbelasting, en het vergroten bepaalt de ooghoek.

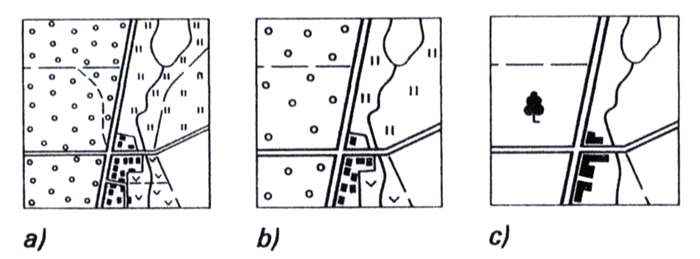
1. Toenemende generalisering (van a naar c) bij gelijkblijvende schaal. De grafische kaartbelasting is in alle drie gevallen bijna exact hetzelfde (8,8 %) terwijl de numerieke kaartbelasting wel duidelijk afneemt (overgenomen uit Töpfer, 1974, p. 79).

Kaartbelasting

Er bestaan drie varianten van het nog jonge begrip kaartbelasting: numerieke, grafische en visuele kaartbelasting. De laatste lijkt vooral van theoretisch belang: "ein hochkomplexer Wert, dessen Beschreibung schon rein verbal erhebliche Schwierigkeiten bereitet." [Koch, 1985] De grafische kaartbelasting - het oppervlak van alle grafische elementen gedeeld door het kaartoppervlak - is eenvoudiger vast te stellen [Töpfer, 1974, p. 81], en kan een nuttig criterium zijn bij het kaartontwerp, maar zoals figuur 1 illustreert wordt de generaliseringsgraad er niet goed door aangegeven. Blijft over de numerieke kaartbelasting B, een simpele en schetsmatige methode, maar eenvoudig te bepalen [Töpfer, 1974, p. 80] en er is geen woord Frans bij:

B=( P + L + V + N ) / O (punten/cm2)

P=aantal puntsymbolen (1 puntsymbool geeft 1 punt)
L=lengte lijnsymbolen (1 cm geeft 1 punt)
V=oppervlak vlaksymbolen (1 cm2 geeft 1 punt)
N=aantal geografische namen (1 naam geeft 1 punt)
O=kaartoppervlak

Figuur 2 geeft een indruk van de kaartinhoud bij verschillende waarden van B.

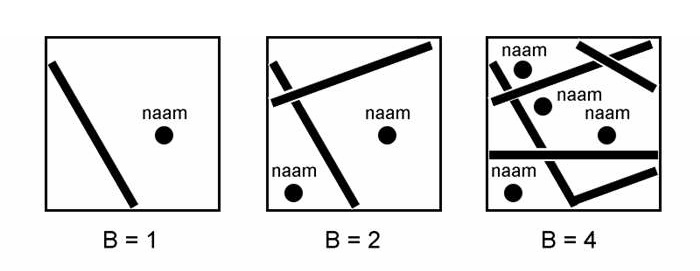
Fig. 2. Kaartinhoud bij verschillende waarden van de numerieke kaartbelasting. Voor een hand- of atlaskaart is B=4 nog acceptabel, voor een schoolwandkaart is deze waarde veel te hoog.

Ooghoek

De ooghoek H is gedefinieerd als de (karakteristieke) afmeting van een puntsymbool of de dikte van een lijnsymbool gedeeld door de leesafstand, dat wil zeggen de afstand tussen het oog en het symbool. [Ormeling, 1997] Dit dimensieloze kengetal is geschikt om de leesbaarheid (het gevormde netvliesbeeld) van symbolen van hand- en atlaskaarten die op normale leesafstand worden gebruikt (in dit artikel 500 mm) te vergelijken met die van wandkaarten met een veel grotere leesafstand (in dit artikel 5000 mm). Uit een minimumgrootte van "Formen durch Linien umgrenzt" van circa 0,35 mm bij normale leesafstand kan een ruwe schatting van een minimumwaarde voor de ooghoek van puntsymbolen worden afgeleid: H_min=0,7 x10^-3. Tabel 1 geeft voor enkele ooghoekwaarden de grootte van cirkelvormige puntsymbolen die op leesafstanden van 500 en 5000 mm hetzelfde netvliesbeeld geven.

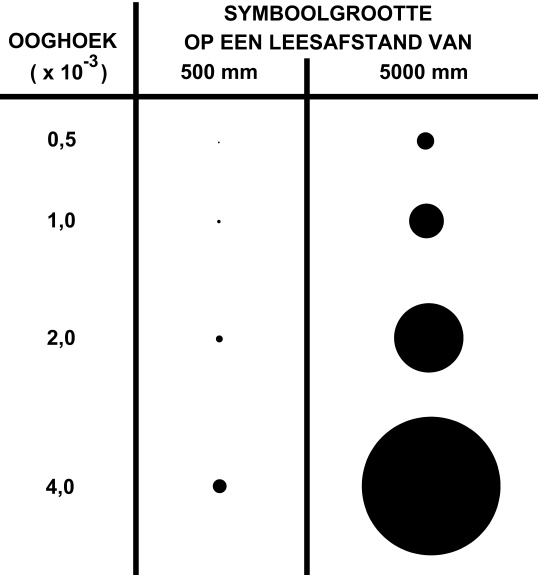
Tabel 1. Ooghoekwaarden van cirkelvormige puntsymbolen op leesafstanden van 500 en 5000 mm.

MUT ZUR WEISEN BESCHRÄNKUNG

Van een groot deel van de beschikbare 19de-eeuwse schoolwandkaarten [Brink, 2007] en van een selectie van de 20ste-eeuwse schoolwandkaarten is de numerieke kaartbelasting bepaald volgens de hierboven beschreven methode. Vlaksymbolen zijn niet in de berekening meegenomen, aangezien vrijwel alle kaarten over het gehele oppervlak op afstand goed zichtbare, zachte grondsoorten-, hoogte- of staatkundige kleuren vertonen, die de andere kaartelementen weinig storen. Van elke kaart is op het oog een karakteristiek gedeelte van circa 600 cm2 van het landgedeelte van de kaart bestemd als 'telgebied' (in het onbelaste zeegedeelte is van generaliseren vrijwel geen sprake). De lengte van lijnsymbolen is bepaald met een curvimeter. De 'telfout' in P, L en N is gering (maximaal 2 %). De belangrijkste meetfout is de keuze van het telgebied, maar de ervaring leert dat een ander karakteristiek telgebied een waarde voor de kaartbelasting oplevert die slechts maximaal 20 % verschilt. Dit doet geen afbreuk aan de nu volgende resultaten.

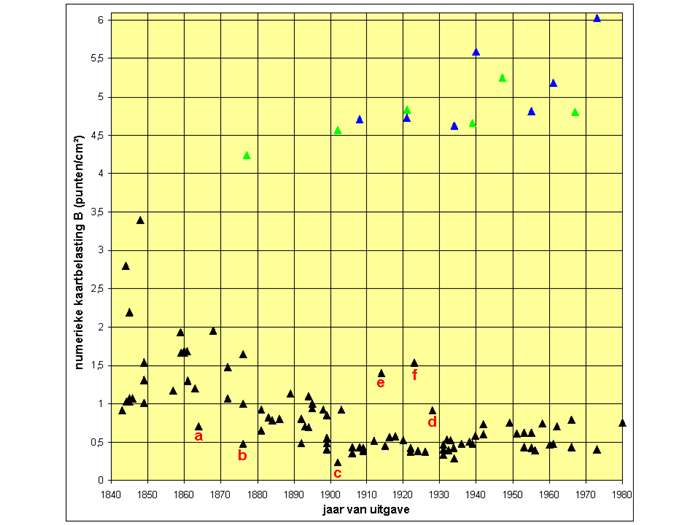
Fig. 3. Numerieke kaartbelasting als functie van de tijd (zwart: schoolwandkaarten, groen: Bosatlas, blauw: Bos-Zeeman atlas).

Figuur 3 geeft de numerieke kaartbelasting van de onderzochte Nederlandse schoolwandkaarten als functie van het jaar van uitgave. Ondanks het feit dat de kaartauteurs van deze schoolwandkaarten een kleurrijke groep eigenwijze en onafhankelijk van elkaar werkende onderwijzers en leraren vormen, valt er toch een trend te ontdekken. De eerste schoolwandkaarten laten een relatief hoge kaartbelasting van 1 à 3 zien. In de loop van de 19de eeuw neemt echter de kaartbelasting af, om vanaf circa 1900 te stabiliseren rond B=0,5. Deze laatste waarde kan dan ook worden gezien als een optimale informatiedichtheid voor schoolwandkaarten. Een illustratie van deze ontwikkeling geeft figuur 4. De op een vergelijkbare manier vastgestelde numerieke kaartbelasting van de overzichtskaart van Nederland in twee zeer bekende schoolatlassen - de Bosatlas en de kleinere en kleinschaligere Bos-Zeeman atlas - ligt rond B=5 (fig. 3). De informatiedichtheid van deze twee atlassen ligt dus circa 10 maal hoger dan die van 20ste-eeuwse schoolwandkaarten. Het gebruik van schoolatlassen op normale leesafstand maakt uiteraard deze hogere kaartbelasting mogelijk. Het door de Franse kartograaf Bertin genoemde maximum van 10 'kaarttekens' per cm2 (ook weer bij normale leesafstand) wordt daarbij niet overschreden. [Bertin, 1974] De licht stijgende trend van zowel atlaskaarten als die van 20ste-eeuwse schoolwandkaarten kan verklaard worden door de uitbreiding van het verkeerswegennet (zie bijvoorbeeld figuur 4c en 4d).

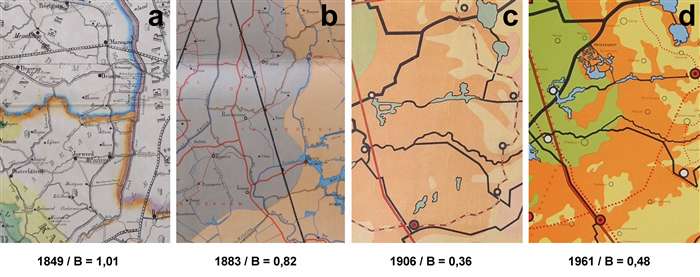
Fig. 4. Vier fragmenten (elk circa 600 cm2) van schoolwandkaarten van de provincie Friesland uit de periode 1849-1961 (FRI_OK_P, FRI_WO1A, FRI_NO1 en FRI_NO5 [Brink, 2007]). De numerieke kaartbelasting laat een dalende trend zien (fragmenten a en b: schaal 1:50.000, collectie Bodel Nijenhuis, Bibliotheek Universiteit Leiden; fragmenten c en d: schaal 1:100.000).

Enkele punten in figuur 3 vallen op door hun afwijkende ligging. De Schoolkaart van het Koningrijk der Nederlanden van C.A.C. Kruyder uit 1864 is van de onderzochte schoolwandkaarten de eerste die in de buurt komt van de optimale B=0,5 (punt a). De kaart valt op door een zwarte landkleur, maar ook door een voor die tijd sobere uitvoering. Volgens recensent J.F. Jansen onderscheidt deze kaart zich positief van al de bestaande schoolwandkaarten, die "te veel en te velerlei bevatten" en met de "gewone landkaarten" een "bijna gelijke uitvoering en uitvoerigheid" gemeen hebben. [Jansen, 1864] Jansen had in 1876 de moed om de kaartbelasting van een door hemzelf ontworpen schoolwandkaart van Utrecht (fig. 5) te laten zakken onder de B=0,5 (punt b). In 1902 wordt zelfs de B=0,25-grens doorbroken door R. Bos met een wel erg lege schoolwandkaart van Frankrijk (punt c; fig. 6). Maar dat kwam hem in die tijd dan ook op een ernstige terechtwijzing te staan: "Zoo generaliseeren als de Heer R. Bos doet, dat is waarlijk te bar." [Niermeyer, 1902] J. Schoonbeek had in 1928 natuurlijk alle recht om zijn schoolwandkaart van Nederland in de uitzonderlijk kleine schaal van 1:400.000 uit te voeren (punt d). Maar om dan toch in deze kleine kaart al de gebruikelijke spoorlijnen, kanalen, rivieren en plaatsen op te nemen getuigde niet van een "Mut zur weisen Beschränkung". [Stollt, 1967]

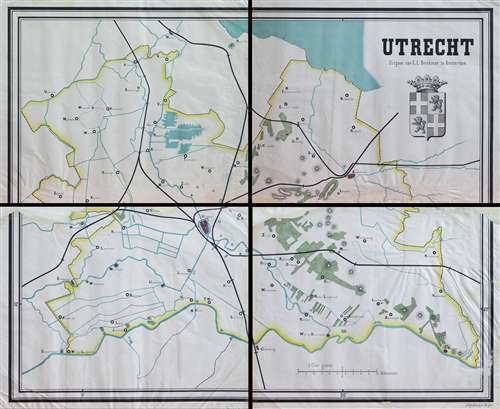
Fig. 5. Schoolwandkaart van Utrecht van J.F. Jansen uit 1876 (punt b in fig. 3) met een voor die tijd lage numerieke kaartbelasting (schaal circa 1:56.000, Bijzondere Collecties, Bibliotheek Universiteit van Amsterdam).

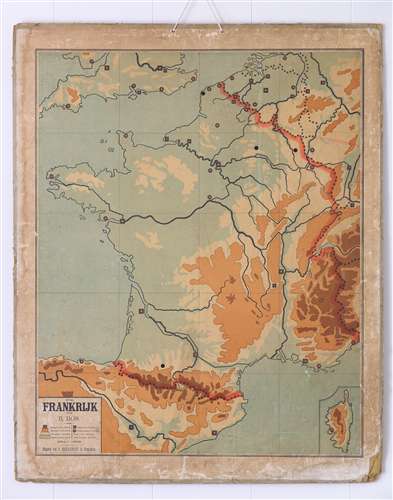
Fig. 6. Schoolwandkaart van Frankrijk van R. Bos uit 1902 (punt c in fig. 3) met een zeer lage numerieke kaartbelasting (schaal 1:1.500.000).

GROBE ART DER DARSTELLUNG

Het meest voorkomende puntsymbool in de Nederlandse schoolwandkaarten is het geometrische (doorgaans cirkelvormige) plaatssymbool. In figuur 7 is de ooghoek van plaatssymbolen in de hierboven al onderzochte schoolwandkaarten gegeven als functie van het jaar van uitgave. Daarbij is steeds de afmeting van het grootste geometrische plaatssymbool in de kaart gebruikt. De onregelmatige symbolen voor de allergrootste steden - 'plattegrondjes' - komen niet in aanmerking voor opmeting aangezien deze als vlaksymbolen zijn te beschouwen. Ter controle zijn ook de ooghoeken van de kleinste geometrische plaatssymbolen bepaald, maar dit laat - ondanks een grotere spreiding - een zelfde trend zien. Figuur 7 geeft duidelijk aan dat de ooghoek van plaatssymbolen steeds maar groter wordt: van H=0,4 à 1,0 x10^-3 voor de eerste kaarten tot een maximum van H=2 à 3 x10^-3 vanaf circa 1930. Schoolwandkaarten werden dus niet alleen steeds leger maar ook steeds grover. Figuur 8 geeft daar een voorbeeld van. De ooghoekwaarden van de grootste plaatssymbolen in de eerste schoolwandkaarten liggen rond H_min, hetgeen aangeeft dat de plaatssymbolen veel te klein getekend zijn (fig. 8a). Kolácný heeft experimenteel vastgesteld dat de minimumgrootte van een cirkelsymbool of een vierkantsymbool bij een leesafstand van 5000 mm, gemiddelde ogen en goed licht circa 6 mm moet bedragen (corresponderend met H=1,2 x10^-3). [Kolácný, 1969b] Pas vanaf circa 1900 voldoen de (grootste) plaatssymbolen aan dit criterium (fig. 8c en 8d).

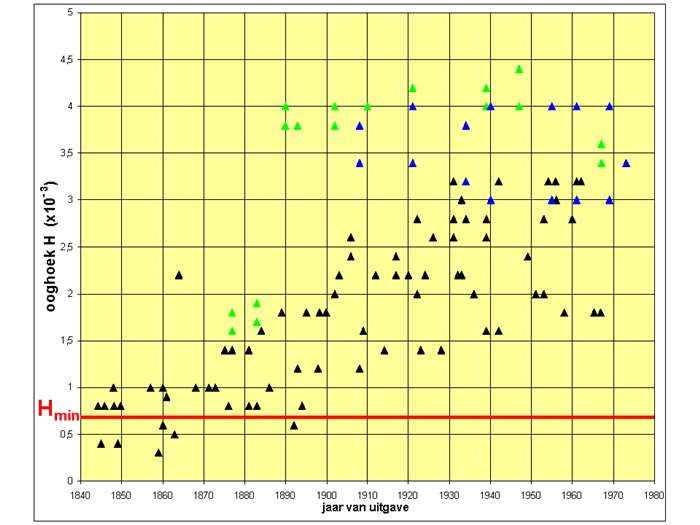
Fig. 7. Ooghoek van de grootste plaatssymbolen als functie van de tijd (zwart: schoolwandkaarten, groen: Bosatlas, blauw: Bos-Zeeman atlas).

In figuur 7 staan ook de ooghoeken vermeld van de grootste plaatssymbolen in de overzichtskaarten van Nederland en van Europa in de twee bovengenoemde schoolatlassen. Afgezien van de (te) lage waarden in de eerste drukken van de Bosatlas zijn deze ooghoeken vrij constant (3 à 4,5 x10^-3). Pas vanaf circa 1930 komen de ooghoeken van schoolwandkaarten in de buurt van die van schoolatlassen.

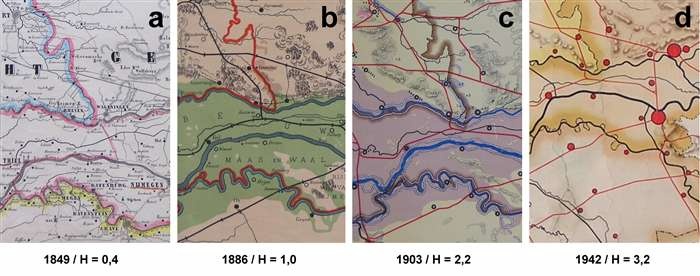
Fig. 8. Vier fragmenten (elk circa 600 cm2) van schoolwandkaarten van Nederland uit de periode 1849-1942 (NED_OK1, NED_WO2S, NED_TB1E en NED_TH3P [Brink, 2007]). De ooghoek laat een stijgende trend zien (fragmenten a en b: schaal circa 1:175.000, collectie Bodel Nijenhuis, Bibliotheek Universiteit Leiden; fragment c: schaal 1:200.000, Bijzondere Collecties, Bibliotheek Universiteit van Amsterdam; fragment d: schaal 1:225.000).

Niet alleen puntsymbolen maar ook lijnsymbolen worden in schoolwandkaarten steeds grover voorgesteld. Door de grote spreiding in de gemeten ooghoeken van de dikste lijnen kan dit het beste worden samengevat als volgt: voor 1900 ooghoek meestal kleiner dan 0,6 x10^-3, na 1900 ooghoek meestal tussen 0,6 en 1,2 x10^-3 (idem dunste lijnen: voor 1900 ooghoek meestal kleiner dan 0,2 x10^-3, na 1900 ooghoek meestal tussen 0,2 en 0,5 x10^-3).

In tegenstelling tot geometrische puntsymbolen zijn er maar enkele voorbeelden van beeldsymbolen in schoolwandkaarten, maar deze passen goed in de trend van figuur 7. De beeldsymbolen in twee kaarten van 1843 en 1844 zijn veel te klein en onleesbaar op afstand. Wat lastig te meten zijn de ooghoekwaarden van afbeeldingen van olifanten, druivetrossen, suikerbieten, paradijsvogels, nylon kousen etc. uit kaarten van 1913 en 1948, maar het is zonneklaar dat deze beeldsymbolen van een voldoende grootte zijn.

AUS DER NÄHE EINE HANDKARTE

De 20ste-eeuwse vervaardiger van een schoolwandkaart - meestal een onderwijzer of leraar - wist wel dat zijn kaart sober moest zijn. Maar sommigen konden daar niet mee uit de voeten. Zo was daar een leraar aan de Rijkskweekschool in Deventer, R. Schuiling, die berucht stond om zijn streven naar volledigheid. Hij nam dan ook veel details op in zijn schoolwandkaart van Nederland uit 1914, hetgeen resulteert in een afwijkende ligging van deze kaart in figuur 3 (B=1,40, punt e) en een kritische opmerking van A.A. Beekman, met wie het toch al niet zo boterde: "De samensteller wachte zich er van alles op te willen voorstellen dat niet noodig is." [Beekman, 1915] Maar vergeleken met de eveneens volle 19de-eeuwse schoolwandkaarten is er met Schuilings kaart iets vreemds aan de hand. Op afstand zijn veel details (zoals kleine plaatsen, beken, tramlijnen, namen) niet meer goed zichtbaar, en blijven de hoofdzaken over (zoals grote plaatsen, rivieren, spoorlijnen). Door gebruik te maken van deze 'optische generalisering' door de ogen van de kaartgebruiker heeft Schuiling getracht een op afstand duidelijke wandkaart te maken, die de kaartgebruiker toch de gelegenheid biedt van dichtbij details op te zoeken. Nog meer is de optische generalisering tot een kunst verheven in R. Noordhoffs Nieuwe wandkaart van Nederland uit 1909, en later vervolmaakt door K. Zeeman (bijvoorbeeld de vierde druk, 1923, punt f in figuur 3). Een fragment van deze kaart van Nijmegen en omgeving (fig. 9 rechts) laat veel details zien: kleine plaatsen, namen, (ontworpen) kanalen, beken, tramlijnen, hoogtecijfers, overlaten, veerboten, etc. Op een afstand verdwijnen deze details en blijven van dit gebied voornamelijk enkele grotere steden, de grote rivieren, spoorlijnen en de grondsoortenkleuring waarneembaar (fig. 9 links). In 1909 werd dit verschijnsel in een recensie al correct opgemerkt: "Op een afstand gezien bemerkt men alleen het voornaamste.Gaat men er echter wat dichter bij staan dan ziet men dat met zachtere tinten zoo wat alles is aangegeven." [N.N., 1909] Het is nog maar de vraag of optische generalisering van wandkaarten een Nederlandse uitvinding is. Ook in Russische wandkaarten schijnt het fenomeen al lang te worden toegepast [Witt, 1970, p. 1063], en in Duitsland is "die kombinierte Hand-Wandkarte" ook niet onbekend: "Die großen zur Verfügung stehenden Flächen bieten die Möglichkeit die Wandkarte mit zarten Zeichnungen inhaltlich so anzureichen, daß sie aus der Nähe betrachtet einer Handkarte gleich kommt." [Painke, 1972]

Fig. 9. Nieuwe wandkaart van Nederland van R. Noordhoff en K. Zeeman uit 1923 (vierde druk, schaal 1:200.000) met rechts een fragment (Nijmegen en omgeving). De vele kaartdetails zijn op grotere afstand vrijwel onzichtbaar.

GENERALISIERUNG DER ERGEBNISSE

Bovenstaande grafieken laten het zwart op wit zien: schoolwandkaarten werden inderdaad steeds soberder. Vooral in de loop van de 19de eeuw werden de kaarten door toenemende generalisering steeds minder belast en leger, en kwam er ruimte vrij voor duidelijkere en grotere symbolen. Een trend die overigens paste in de ontwikkeling van het aardrijkskunde-onderwijs in die tijd naar minder details en meer inzicht. Het benadrukken van de afstandswerking door Ten Have en Zondervan in de jaren '90 van de 19de eeuw was toen zeker nog nodig, maar de trend naar sobere wandkaarten was in feite al eerder ingezet. De leesbaarheid van schoolwandkaarten nam zienderogen toe: een legere kaart was het medicijn tegen de grauwsluier van de eerste kaarten, en de toepassing van grotere symbolen was een middel om een duidelijke contrastwerking te krijgen.

Als de trends in de kaartbelasting van schoolatlaskaarten en schoolwandkaarten geëxtrapoleerd worden in de richting van het jaar 1800, dan lijkt het erop dat deze twee kaarttypen een gezamenlijke voorouder bezitten: de al of niet in aardrijkskundige leerboeken opgenomen, van dichtbij te gebruiken schoolkaartjes uit de 18de eeuw en het begin van de 19de eeuw. [Brink en Holl, 2010, p. 10-16] De schoolwandkaart voelde - in tegenstelling tot de schoolatlaskaart - echter maar weinig affiniteit voor deze voorouder. Hij ontwikkelde zich door de hierboven geschetste generalisering in de loop van de 19de eeuw tot een kaart van een geheel nieuw type - de op grote afstand leesbare wandkaart - en wist zich bijgevolg los te maken uit het keurslijf van de op kleine afstand leesbare kaarten zoals atlaskaarten en kantoorwandkaarten.

Deze 'uitvinding' had echter wel een groot deel van de 19de eeuw nodig om terrein te winnen. De kaartauteurs hadden vrijwel geen contact met elkaar, en bij elke nieuwe schoolwandkaart moest opnieuw het wiel worden uitgevonden. Bovendien ontbrak ook vaak de durf om af te wijken van bestaande kaarten: "Es gehört schon einigen Mut dazu ein so leeres, abstrahiertes Erdabbild als fertiges kartographisches Produkt anzubieten." [Stollt, 1967] De toepassing van zeer grote puntsymbolen (circa 15 mm) vraagt blijkbaar nog meer lef dan het ontwerpen van lege kaarten, aangezien deze symbolen pas vanaf circa 1930 getoond durven te worden. Het verschijnen van deze knoepers van symbolen in de Nederlandse schoolwandkaarten heeft de langdurige strijd tussen volledigheid en duidelijkheid definitief in het voordeel van de laatste beslist.




Literatuur

-Beekman, A.A., Nieuwe schoolkaarten van Nederland. - In: Tijdschrift van het Kon. Nederlandsch Aardrijkskundig Genootschap XXXII (1915), p. 678-683. - citaat p. 681.

-Bertin, J., Graphische Semiologie: Diagramme Netze Karten. - Berlin, 1974. - p. 183-189.

-Bobek, H., Gesamtanlage und Einzelgestaltung. - In: Grundsatzfragen der Kartographie. - Wien, 1970. - p. 62.

-Brink, L.E.S., Bibliografie en foto-overzicht van de Nederlandse schoolwandkaarten (1801-1975). - Nijmegen, 2007.

-Brink, L.E.S. en L.M.A. Holl, De wereld aan de wand: de geschiedenis van de Nederlandse schoolwandkaarten. - Zwolle, 2010.

-Commissie heruitgave Topographische en Militaire Kaart, Heruitgave van de eerste editie van de 'Topographische en Militaire Kaart van het Koningrijk der Nederlanden'. - In: Geografisch Tijdschrift - Nieuwe Reeks VII (1973), p. 383-388. - citaat p. 384.

-Eckert, M., Die Kartenwissenschaft: Forschungen und Grundlagen zu einer Kartographie als Wissenschaft. - Berlin, 1921. - deel I, p. 332 en 339.

-Hettner, A., Die Eigenschaften und Methoden der kartographischen Darstellung. - In: Internationales Jahrbuch für Kartographie II (1962), p. 13-35. - herdruk van artikel uit 1910, citaat p. 18.

-Imhof, E., Die Kunst in der Kartographie. - In: Internationales Jahrbuch für Kartographie VII (1967), p. 21-32. - citaat p. 26.

-Imhof, E., Thematische Kartographie. - Berlin, 1972. - p. 220.

-Jansen, J.F., Schoolkaart van het Koningrijk der Nederlanden. - In: Nieuwe Bijdragen ter Bevordering van het Onderwijs en de Opvoeding etc. (1864), 654-656. - citaat p. 655.

-Koch, W.G., Zur Erforschung von Gesetzmäßigkeiten der visuellen Kartenbelastung. - In: Fortschritte in der geographischen Kartographie. - Gotha, 1985. - p. 330.

-Kolácný, A., Cartographic information: a fundamental concept and term in modern cartography. - In: Cartographic Journal 6 (1969a), p. 47-49. - citaat p. 47.

-Kolácný, A., Utilitarian cartography: the road toward the optimal effect of cartographic information. - Prague, 1969b. - ICA Working Group paper, p. 20-21.

-Niermeyer, J.F., De tentoonstellingen in Antwerpen en in Amsterdam. - In: Tijdschrift van het Kon. Nederlandsch Aardrijkskundig Genootschap XIX (1902), p. 856-869. - citaat p. 865.

-N.N., Over kaarten voor de natuurkundige geographie etc. - In: Nieuwe Bijdragen ter Bevordering van het Onderwijs en de Opvoeding etc. (1853), 23-29. - citaat p. 24.

-N.N., Nieuwe wandkaart van Nederland. - In: Het Katholieke Schoolblad 2 (1909), p. 182.

-Ormeling, F.J., Verslag studiedagen kartografische kommunikatie. - [Groningen], 1972. - p. 2.

-Ormeling, F.J., Kartografische grammatica: de grafische variabelen. - In: Kartografisch Tijdschrift XXIII (1997), nr. 4, kernkatern 8, p. 32.

-Ormeling, F.J. en M.J. Kraak, Kartografie: ontwerp, produktie en gebruik van kaarten. - Delft, 1987. - p. 58-67.

-Painke, W., Haacks Wandatlanten gestern und heute. - In: Kartographische Nachrichten 22 (1972), p. 180-183. - citaat p. 182.

-Sperling, W., Wandkarte, Schulwandkarte. - In: Handbuch Medien im Geographie-Unterricht. - Düsseldorf, 1986. - p. 149-150.

-Stollt, O., Der Fortlauf der Generalisierung durch die Maßstabsfolge. - In: Kartographische Generalisierung: Ergebnisse des 6. Arbeitskurses Niederdollendorf etc. - Mannheim, 1967. - Textband, p. 40.

-Sydow, E. von, Drei Karten-Klippen. - In: Geographisches Jahrbuch I (1866), p. 348-361. - citaat p. 358.

-Töpfer, F., Kartographische Generalisierung. - Gotha, 1974.

-Veth, P.J., Populaire aardrijkskunde in ons vaderland. - In: De Gids 16 (1852), II, 529-561. - citaat p. 538.

-Witt, W., Thematische Kartographie. - Hannover, 1970, 2e druk.



Samenvatting

Van kaart aan de wand naar wandkaart:
Generalisering van schoolwandkaarten vanaf 1840

Al eerder geuite veronderstellingen dat de vanaf circa 1840 in gebruik gekomen Nederlandse schoolwandkaarten steeds soberder en duidelijker werden uitgevoerd, zijn voor het eerst kwantitatief bevestigd. Uit metingen van de numerieke kaartbelasting volgt dat vooral in de loop van de 19de eeuw de schoolwandkaarten steeds leger werden. Uit ooghoekmetingen van punt- en lijnsymbolen blijkt dat de symbolen in deze kaarten tot circa 1930 steeds groter en dikker getekend werden. Door deze specifieke vorm van generalisering ontstond er geleidelijk een geheel nieuw kaarttype: de op afstand leesbare wandkaart.